如何理解笛卡尔积、外积、内积？

笛卡尔积

笛卡尔乘积是指在数学中，两个集合X和Y的笛卡尓积（Cartesian product），又称直积，表示为X×Y，第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员 。

例如，A={a,b}, B={0,1,2}，则

A×B={(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}

内积inner productor点积dot product

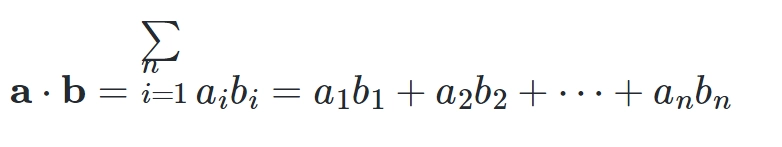
外积outer product

给定两个向量和

它们的外积 定义为 m x n的矩阵 $$ \mathbf{u} \otimes \mathbf{v}=\mathbf{A}=\left[\begin{array}{cccc}{u_{1} v_{1}} & {u_{1} v_{2}} & {\ldots} & {u_{1} v_{n}} \ {u_{2} v_{1}} & {u_{2} v_{2}} & {\ldots} & {u_{2} v_{n}} \ {\vdots} & {\vdots} & {\ddots} & {\vdots} \ {u_{m} v_{1}} & {u_{m} v_{2}} & {\ldots} & {u_{m} v_{n}}\end{array}\right] $$ 或者用index表示为 $(\mathbf{u} \otimes \mathbf{v}){i j}=u{i} v_{j}$

内积为外积矩阵的迹

以下是矩阵的运算

哈达玛积Hadamard product（又称作逐元素积）） $$ \mathbf{A} \circ \mathbf{B}=\left[\begin{array}{cccc}{a_{1,1} b_{1,1}} & {a_{1,2} b_{1,2}} & {\cdots} & {a_{1, n} b_{1, n}} \ {a_{2,1} b_{2,1}} & {a_{2,2} b_{2,2}} & {\cdots} & {a_{2, n} b_{2, n}} \ {\vdots} & {\vdots} & {\ddots} & {\vdots} \ {a_{m, 1} b_{m, 1}} & {a_{m, 2} b_{m, 2}} & {\cdots} & {a_{m, n_{1}} b_{m, n}}\end{array}\right] $$